量子化学計算プログラムのGAMESSで分極率を計算します。
入力ファイルはこちらです。
$CONTRL
DFTTYP=B3LYP
RUNTYP=FFIELD
MULT=1
SCFTYP=RHF
$END
$BASIS
GBASIS=N31
NGAUSS=6
NDFUNC=1
$END
$DATA
CH4
C1
C 6 -3.7822025540019e-07 2.3465437752871e-08 -7.5497392094087e-07
H 1 6.3134086618702e-01 6.3134059613857e-01 6.3134113770467e-01
H 1 -6.3134064882349e-01 -6.3134091006717e-01 6.3134140907342e-01
H 1 6.3134143681325e-01 -6.3134121079123e-01 -6.3134073012910e-01
H 1 -6.3134127815771e-01 6.3134149610957e-01 -6.3134106094046e-01
$ENDASEでCH4分子の構造最適化をした際に残っていたファイルが元になっています。
書き換えたのはRUNTYP=FFIELDの部分です。
FFIELDの説明は、
= FFIELD applies finite electric fields, most commonly to extract polarizabilities.
https://www.msg.chem.iastate.edu/gamess/GAMESS_Manual/docs-input.txt
ということで、電場をかけて分極率を出してくれます。
計算結果を見るといろんな方向から電場をかけている様子が分かると思います。
そして計算結果の最後の部分。
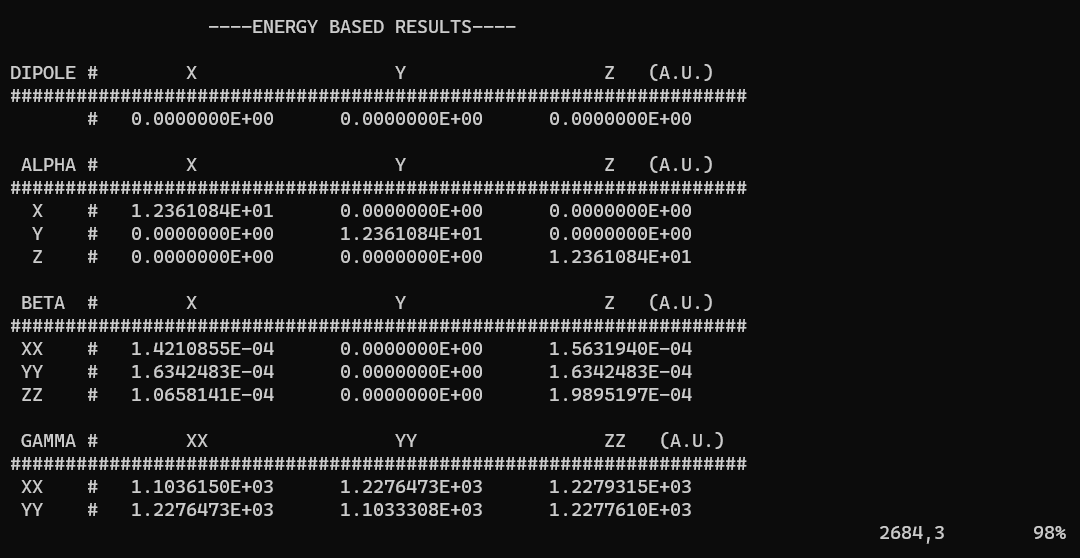
----ENERGY BASED RESULTS----
DIPOLE # X Y Z (A.U.)
###################################################################
# 0.0000000E+00 0.0000000E+00 0.0000000E+00
ALPHA # X Y Z (A.U.)
###################################################################
X # 1.2361084E+01 0.0000000E+00 0.0000000E+00
Y # 0.0000000E+00 1.2361084E+01 0.0000000E+00
Z # 0.0000000E+00 0.0000000E+00 1.2361084E+01
:
:
:
----DIPOLE BASED RESULTS----
DIPOLE # X Y Z (A.U.)
###################################################################
# 0.0000000E+00 0.0000000E+00 0.0000000E+00
ALPHA # X Y Z (A.U.)
###################################################################
X # 1.2361508E+01 0.0000000E+00 0.0000000E+00
Y # 0.0000000E+00 1.2361510E+01 0.0000000E+00
Z # 0.0000000E+00 0.0000000E+00 1.2361517E+01このALPHAが分極率です。
ENERGY BASEDとDIPOLE BASEDの2種類がありますが、2通りの計算をして精度を確認できるということなんだと思います。
この部分をMOPACの計算と比較してみます。
GAMESS
| 12.361084 | 0.0 | 0.0 |
| 0.0 | 12.361084 | 0.0 |
| 0.0 | 0.0 | 12.361084 |
MOPAC POLAR
| 17.7913 | 0.0 | 0.0 |
| 0.0 | 17.7913 | 0.0 |
| 0.0 | 0.0 | 17.7910 |
ISOTROPIC AVERAGE ALPHA
= 17.79119 A.U. = 2.63638 ANG.**3
こんな感じで値は違いますがオーダーは近いです。
またMOPACのほうには単位換算した分極率が書かれています。
2.63638Å3は実際の分極率(2.6Å)と一致しています。
ISOTROPIC AVERAGE ALPHAはテンソルの対角成分の平均値になっています。
GAMESSのほうの単位は書かれていませんが、MOPACと同じ換算をしていると仮定します。
17.79119 A.U.=2.63638Å3は数値が0.14818倍違いますが、これは原子単位系(atomic unit)の長さ 1 a.u. = 0.5291772 Åを3乗したもの、0.52917723=0.14818と一致します。
なのでGAMESSの結果も同じように計算すると、1.83Å3となります。ちょっと小さいですね。
というかこの考え方で合っているんですかね?
詳しい方がいらっしゃいましたらコメントで教えてください。
何か分かったら記事に追記します。
コメント