溶液の混ざりやすさの指標になる溶解度パラメータ(Hildebrand溶解度パラメータ、溶解パラメータ、SP値)をLAMMPSで計算してみます。
原理
溶解度パラメータδ は凝集エネルギーEcohから計算できます。凝集系の分子数を100個とした場合、
$$
E_{coh} = (E_{1} \times 100 – E_{100} ) / 100
$$
$$
\delta = \sqrt{\frac{E_{coh}}{V}}
$$
Ecoh 凝集エネルギー[cal]
δ 溶解度パラメータ [(cal/cm3)1/2]
V モル体積[cm3]
凝集エネルギーは、凝集状態のポテンシャルエネルギーと孤立状態のポテンシャルエネルギーの差です。凝集状態と孤立状態の1分子当たりの分子間力の差を見ていると言い換えることもできます。また、凝集状態から孤立状態に変化させるために必要なエネルギーになるため、気化エネルギーと呼ばれることもあります。
モル体積は物質1molの体積です。
分子100個のMD計算と分子1個のMD計算のポテンシャルエネルギーをそれぞれE100 E1として、上記の式のように、分子1個当たりの凝集状態・孤立状態のエネルギー差を計算します。
計算内容
OpenFFを使ってエタノールのMD計算を2種類実行します。
こちらの記事の方法で、エタノールが1分子のMD計算とエタノールが100分子のMD計算を行います。
1分子のサンプルはNVTアンサンブルで計算します。
100分子のサンプルはNPTアンサンブルで密度を安定させてからNVTアンサンブルで計算します。
温度 298.0 K、NPT圧力は1気圧、時間刻みは0.5 fsで、各計算は10万step実行しました。
結果
各サンプルのポテンシャルエネルギーの平均値は次の通りです。
| PotEng [kcal/mol] | |
|---|---|
| 1分子 | 2.462 |
| 100分子 | -406.284 |
Ecoh = { (2.462 ×100) – (-406.284) } / 100 = 6.525 [kcal/mol] = 6525 [cal/mol]
そして100分子のほうの密度が0.772g/cm3、またエタノールの分子量が46.068 g/molなので、1モルの体積は46.068/0.772= 59.674 [cm3]
$$
\delta = \sqrt{\frac{E_{coh}}{V}} = \sqrt{\frac{6525}{59.674}} = 10.46
$$
エタノールの溶解度パラメータは 10.46 [(cal/cm3)1/2] という結果になりました。(ちなみに単位をジュール [(J/cm3)1/2] に変えると√4.184≒2倍 大きい値になります)
Wikipedia調べではエタノールの溶解度パラメータは 12.7 [(cal/cm3)1/2]です。結構近い結果になったと思います。OpenFF、すごいです。
凝集状態の計算では分子数が100でしたが、これをもっと増やすことで結果は変わるかもしれません。またエタノールの実際の密度は 0.789 g/cm3 なのに対し、今回の計算では0.772です。実際よりも密度が低いことも、溶解度パラメータが低くなった原因かもしれません。
まとめ
LAMMPSを使ってエタノールの溶解度パラメータを計算しました。計算自体は単純ですが、単位変換に気を付ける必要があります。
補足
溶解度パラメータはポリマーでも使用されることがあるようですが、この計算方法はポリマーでは上手く計算できない可能性があります。今回の計算は低分子だったため、孤立状態のMD計算は分子間力が働かない状態、凝集状態は分子間力が働いている状態です。1分子当たりのポテンシャルエネルギーの差を計算したことは、この分子間力の差を計算したことになります。ポリマーのような長い分子は自分自身に絡みつくことができるため、孤立状態のMDでも自分自身に分子間力が働いてしまいます。凝集状態においてもその影響はありそうです。したがって、今回の方法でポリマーの凝集エネルギーを計算すると精度が悪い可能性があります。
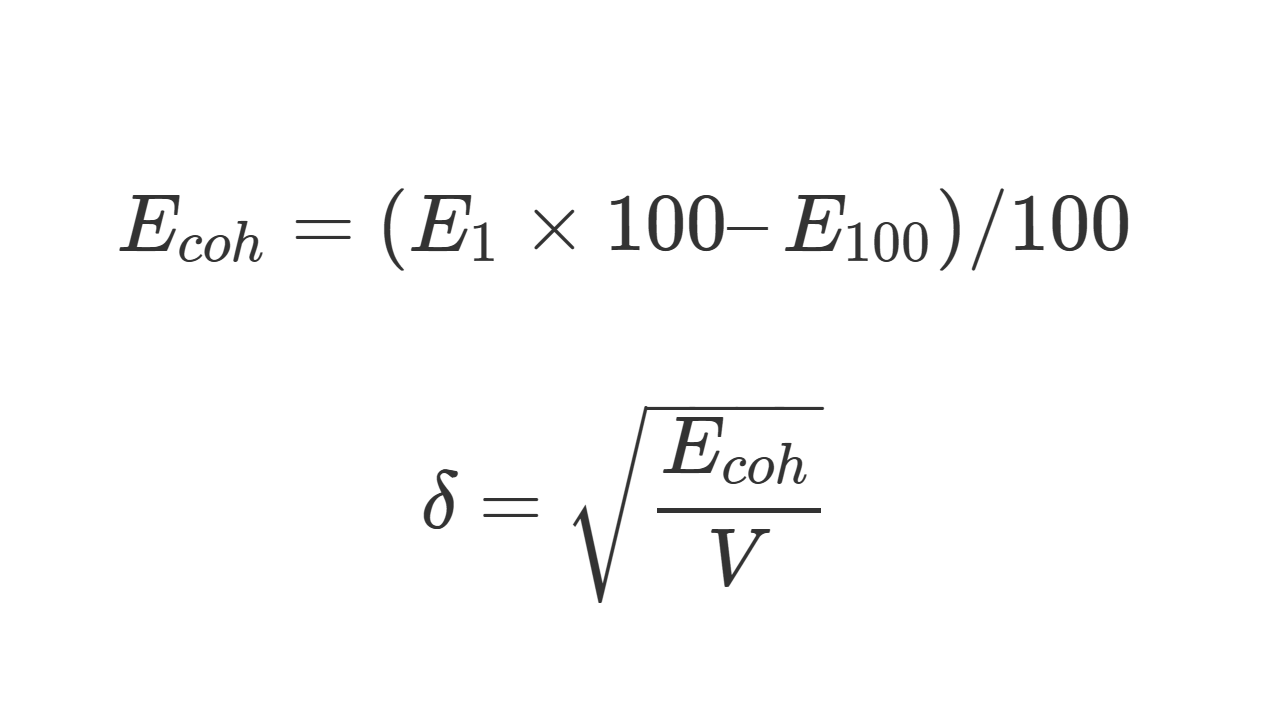

コメント