分子動力学法の解析でよく使う自己相関関数をPythonで書きます。
Green-Kubo公式
自己相関関数は何に使うか?というとGreen-Kubo公式で使います。
速度自己相関関数から自己拡散係数が分かるとか、圧力の自己相関関数から粘度が分かるとか、そいういうものです。
$$
\eta = \frac{V}{k_BT} \int_0^\infty \langle P_{xy}(0)P_{xy}(t) \rangle \, dt
$$
この式の< >の中の部分です。
積分の内側で、時刻=0の時の値と時刻=tの時の値の積を計算して平均しています。
これを積分したものが自己拡散係数や粘度になります。
NumPyでの書き方
自己相関関数(auto-correlation function)をNumPyで書くとこんな感じです。
import numpy as np
def auto_correlation(x):
corre = np.correlate(x, x, "full")
return corre[int(corre.size/2):] / np.arange(len(x), 0, -1)
これだけです。(ちなみに大きい配列ではscipy.signal.correlateを使ったほうが速いらしいです)
何をしているのか、下の例で説明します。
>>> a
array([1, 2, 3])
>>> np.correlate(a,a,"full")
array([ 3, 8, 14, 8, 3])
>>> auto_correlation(a)
array([4.66666667, 4. , 3. ])配列aに[1, 2, 3]という値が入っています。
これをnp.correlateすると[ 3, 8, 14, 8, 3]が返ってきます。
左右対称なので右半分に着目すると[14, 8, 3]です。
14 = 1*1 + 2*2 + 3*3
8 = 1*2 + 2*3
3 = 1*3
という計算から出てきたもので、表で書くと上の段と下の段の掛け算の形になっています。
| 1 | 2 | 3 |
| 1 | 2 | 3 |
| → | 1 | 2 | 3 |
| 1 | 2 | 3 |
| → | → | 1 | 2 | 3 |
| 1 | 2 | 3 |
このように、np.correlateでは同じ配列を一つずつシフトして掛け算しています。
次にauto_correlateの中身です。返り値は[4.66666667, 4. , 3. ]です。
前述のように、0個シフトの場合は3つの掛け算、1個シフトは2つの掛け算、2個シフトは1つの掛け算です。
これを1つあたりに直したものをauto_correlateで返しています。
4.666 = 14.0 / 3
4 = 8.0 / 2
3 = 3.0 / 1 ということです。
追記
上記のコードでは入力データの長さと同じ長さの出力になりますが、長いデータでは計算に時間がかかります。
入力データは長いけど出力は短くていいという場合は以下の書き方のほうが速いです。
def auto_correlation(x, lim):
n = len(x)
y = np.zeros(lim)
y[0] = np.sum(x*x)/n
for i in range(1, lim):
xx = x[0:-i] * x[i:]
y[i] = np.sum(xx) / len(xx)
return y入力の配列がx、出力の長さがlimです。
長さが10万の配列で出力が5000個だけ欲しい場合、先ほどのコードとこのコードでは10倍くらい速度が変わりました。
つまりどういうこと?
$$
\eta = \frac{V}{k_BT} \int_0^\infty \langle P_{xy}(0)P_{xy}(t) \rangle \, dt
$$
この式の
$$
\langle P_{xy}(0)P_{xy}(t) \rangle
$$
の部分の計算です。
P(0) × P(t) の掛け算を、tを1つずつ増やしながら実行する。
これは、先ほどの表のように1つずつシフトして掛け算して、それを< >で平均するということです。
| 1 | 2 | 3 |
| 1 | 2 | 3 |
| → | 1 | 2 | 3 |
| 1 | 2 | 3 |
| → | → | 1 | 2 | 3 |
| 1 | 2 | 3 |
NumPyで書いたauto_correlationの動きの通りです。
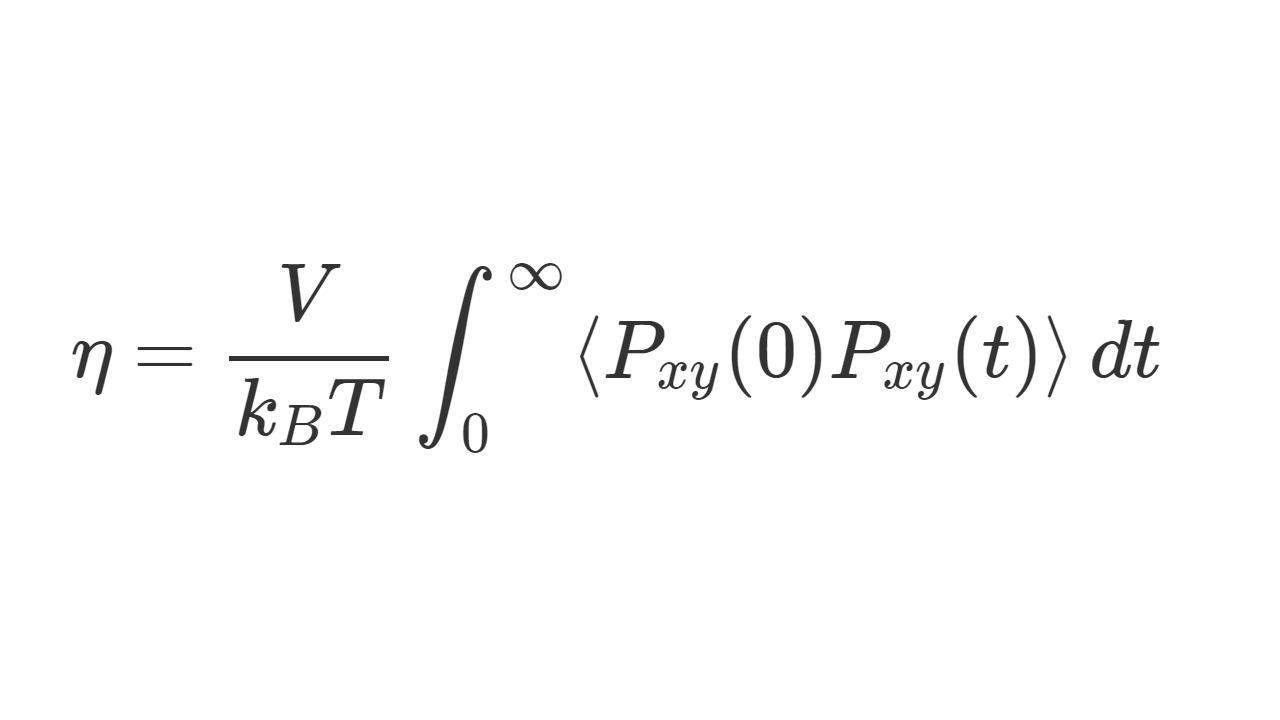
コメント