分子動力学法プログラムのLAMMPSを使って水の粘性係数を計算します。
Green-Kubo公式
$$
\eta = \frac{V}{k_BT} \int_0^\infty \langle P_{xy}(0)P_{xy}(t) \rangle \, dt
$$
こちらの式を使います。
kBはボルツマン定数、Tは温度、Pxyは圧力テンソルの非等方成分です。
このPxyの自己相関関数を計算して積分します。なお実際はPxyだけでなくPyzやPxzも使います。
自己相関関数についてはこちらで解説しています。
使用するデータ
水の計算をした際のデータを使用します。
この計算の最後でwrite_data spce.dataをしています。
これによって密度緩和を終えた構造データが保存されていますので、これを初期構造にしてNVTアンサンブルの計算をします。
units real
atom_style full
read_data spce.data
mass 1 15.9994
mass 2 1.008
pair_style lj/cut/coul/long 10.0 10.0
pair_coeff 1 1 0.1553 3.166
pair_coeff 1 2 0.0 1.0
pair_coeff 2 2 0.0 1.0
kspace_style ewald 1.0e-4
bond_style zero
bond_coeff 1 1.0
angle_style zero
angle_coeff 1 109.47
timestep 1.0
fix rigid all shake 0.0001 20 0 b 1 a 1
fix integrate all nvt temp 298.0 298.0 100.0
thermo_style custom step temp press etotal pe ke
thermo 1000
variable pxy equal pxy
variable pyz equal pyz
variable pxz equal pxz
fix pwrite all print 1 "${pxy} ${pyz} ${pxz}" screen no file pxy.dat
run 100000 upto
print "****Volume ${vol}"トラジェクトリは不要なのでdumpを消しています。必要なら書き加えてください。
そして大事なのは赤い部分で、ここで圧力テンソルの非対角成分を1step毎にファイル pxy.dat に書き出します。
最終行では体積をログに出力するようにしています。
これは粘度を求める式で使用しますが、上手い出力方法が思いつかなかったのでこうしています。
解析
この計算で生成されるpxy.datとlog.lammpsをPythonで読み込んで計算します。
import numpy as np
kB = 1.380649e-23
T = 298.0 #[K]
dt = 1.0 *1e-15 #[s]
tmax = 5000 #[step]
#圧力データの読み込み
data = np.genfromtxt("pxy.dat")
#体積の読み込み
f = open("log.lammps", "r")
lines = f.readlines()
f.close()
for line in lines:
if "****Volume" in line:
line_data = line.split()
V = float(line_data[1]) #[A3]
#[A3] -> [m3]
V = V * 1e-30
#[atm] -> [Pa]
p1 = data[:,0] *101325.0 #Pxy [Pa]
p2 = data[:,1] *101325.0 #Pyz [Pa]
p3 = data[:,2] *101325.0 #Pxz [Pa]
#自己相関関数
def auto_correlation(x, lim):
n = len(x)
y = np.zeros(lim)
y[0] = np.sum(x*x)/n
for i in range(1, lim):
xx = x[0:-i] * x[i:]
y[i] = np.sum(xx) / len(xx)
return y
#Pxy, Pyz, Pxzの自己相関関数
ac1 = auto_correlation(p1, tmax)
ac2 = auto_correlation(p2, tmax)
ac3 = auto_correlation(p3, tmax)
#3つそれぞれを積分
integral1 = np.trapz(ac1) *dt
integral2 = np.trapz(ac2) *dt
integral3 = np.trapz(ac3) *dt
#xy, yz, xzの平均を取って粘度を計算
integral = (integral1 + integral2 + integral3) / 3.0
viscosity = V /(kB*T) * integral
print("Viscosity= %15.6f [Pa.s] %15.3f [mPa.s]"%(viscosity, viscosity*1000))結果はこうなります。
$ python3 acf.py
Viscosity= 0.000779 [Pa.s] 0.779 [mPa.s]常温常圧の水の粘度が 0.779 mPa s(0.779 cP)という結果になりました。
実際の水は0.89 mPa s なので、非常に良い結果だと思います。
ちなみに圧力テンソルの非対角成分の自己相関関数はこんな感じです。
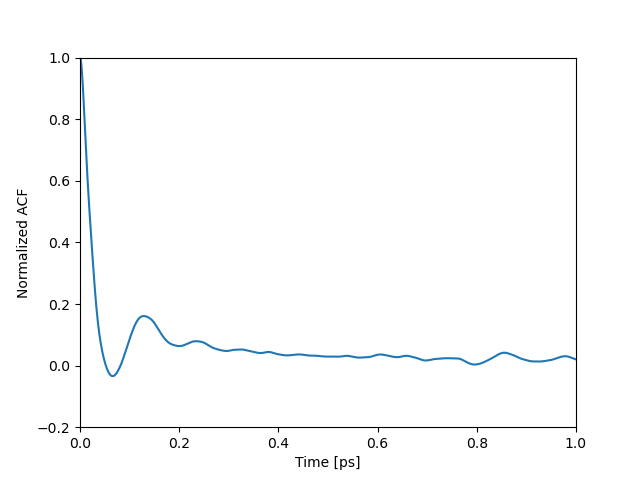
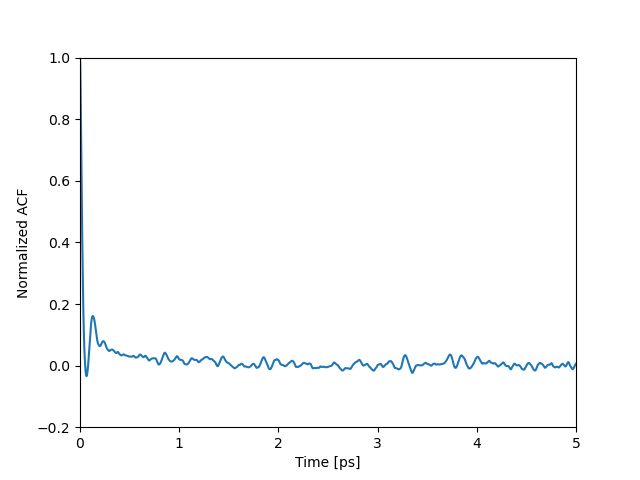
3つある自己相関関数を平均し、縦軸は最大値を1.0としてノーマライズし、時間範囲を1.0psまでと5.0psまででプロットしました。
今回はtmax=5000[step]、つまり5.0psで十分に収束したということにして積分を打ち切っています。
同様のことをやっている論文を見ると4.5psくらいで打ち切っていました。
また、自己相関関数を計算する部分をnp.correlateを使ったところ結構遅くなりました。
10万点のデータの自己相関関数をまじめに計算するよりも、上記のコードのように必要な5000step分の自己相関関数をループで計算したほうが速かったです。
まとめ
水の粘度を計算してみました。精度よく計算できました。

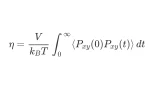
コメント